The Arduino as a simple JTAG adapter

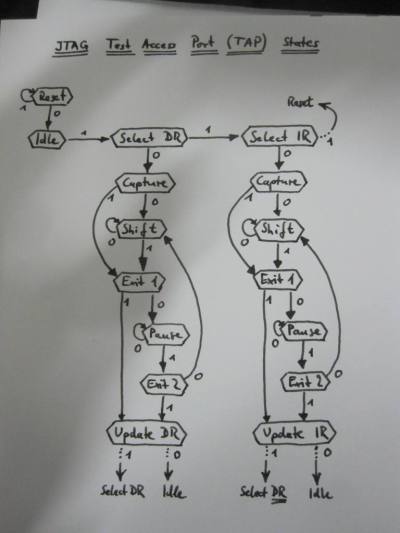
A good while ago I won one of the free PCBs regularly given away by DIY hardware shop Dangerous Prototypes. My board of choice was a CPLD breakout board, for the Xilinx XC9572XL. CPLDs are the smaller brother of FPGAs: programmable logic chips that can be made to act as any integrated circuit within the device's limits. The XC9572XL is programmed via a standard JTAG interface. I did not have anything that speaks JTAG so went looking if my Arduino can be turned into an appropriate programmer. The solution that I found, however, did not work; so I built my own.

Normally, to program a CPLD, or FPGA, one buys an expensive interface cable and uses it with the software development suite supplied by the particular chip's vendor. Of course there are plenty of DIY alternatives; in fact, Dangerous Prototypes sell one or two. One of my goals with this project was, however, to spend next to no money on it. I got the circuit board for free, the parts cost around 3EUR, and I had already done a similar job with my Arduino Atmel programmer.

So after soldering the board I flashed the abovementioned JTAG code onto the Arduino. This was my second time SMD-soldering so I was not expecting the board to work on first try. But even after checking every connection with a multimeter, JTAGWhisperer would do apparently nothing after receiving the first chunk of data. I eventually gave up searching for the cause.

Instead I decided to write a very simple Arduino program that allows direct interaction with the JTAG interface from a serial terminal. It is called jtagbang because it is essentially bit-banging on the JTAG pins. By pure coincidence, it also requires frequent use of the exclamation mark (bang) when talking to it.

I didn't know anything about JTAG until three days ago. Now I know that it is awesome. The point of JTAG is to connect to any number of chips in some circuit design, taking up next to no space on the board, requiring only very simple support from the chip, and allowing the user to inspect and manipulate virtually every pin and connection at any time without touching anything. I call it fucking magic.

These LEDs are lit because I told the chip I needed those outputs on for testing purposes.

Unfortunately I cannot explain the magic in the space of this post, however, here is a link to the IEEE specification. While IEEE doesn't want you to read their standards, someone has helpfully put the 2001 version on slideshare… Reading that spec is still not much fun, but I made a drawing of the important part.

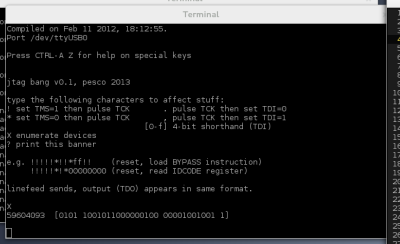
So, long story short: Upload the attached sketch to an Arduino, take a peek at the top of the file maybe, and connect to it with a terminal emulator (read minicom) or the Arduino IDE's serial monitor (set to line-ending Newline). Enter a capital X and it will interrogate the JTAG interface to find all the connected devices (chips). It lists their built-in identification codes which take the form of 32 bits in four groups:

59604093  [0101 1001011000000100 00001001001 1]

The groups are, from most to least significant bit: 4-bit product version (5), 16-bit product code (9604 is the XC9572XL), 11-bit manufacturer code (00001001001 is Xilinx), and one bit that is always 1 for thaumaturgic reasons.

I should find a PC mainboard to try this with.

Next, I need to get the CPLD programmed. Xilinx uses (X)SVF files for this, a file format that describes what to do on a JTAG interface in a more high-level fashion than my bit-banging. I need a player for this format that translates standard SVF commands into bang language and vice-versa. The good thing is that I can now do this in a high-level programming language of my choice entirely on the host instead of cramming it into the Arduino.

The adventure after that will be learning VHDL and designing an actual integrated circuit.

Attachment: jtagbang.ino (v0.1)

I am releasing the code under the terms of the quite permissive ISC license.

JSON with blobs, still context-free

Pen and paper design.

Inspired by their talk The Science of Insecurity I took Meredith Patterson and Sergey Bratus by their word and tried to solve my next network communication problem without crossing the line beyond deterministic context-free languages.

The upshot of said talk was that most if not all security problems stem from the fact that some software component could not foresee the consequences of its input. From a language-theoretic point of view, the problem boils down to recognizing the set (language) of acceptable inputs. There are different classes of languages whose recognizers require increasingly complex mechanisms. Things are basically pleasant with regular languages and one step up, aforementioned deterministic context-free ones. Up to this point we can algorithmically decide whether two specifications describe the same language; whether two peers in the network are cleanly interoperable.

When I was looking for a good data serialization format, in addition to my original requirements, I went looking for one that had a deterministic context-free grammar. Incidentally, one of the things I wanted to be able to do was efficiently transfer relatively large blocks of arbitrary data. Unfortunately, what immediately catapults you into the land of (mildly) context-sensitive languages are length fields.

JSON (as implied by the title) would have been my favorite choice, but the best way to put binary blobs in it is by encoding them as Base64-encoded strings.

{ "message":    "Hi, Bob!"
, "attachment": "ZGFmdXFpc3RoaXM="
}

For one thing, this means overhead in encoding time, decoding time and data volume. Also it is unsatisfying because one property of JSON is self-descriptiveness: recognizing a JSON value reveals its type. Base64 blobs would be hidden in strings and force the recipient to know exactly where to expect them.

A short note about overhead and efficiency concerns. It is generally rightfully considered foolish to optimize prematurely. From most standpoints, computers are fast, bandwidth is cheap and you are probably wasting ten times as much elsewhere as avoiding Base64 would ever save. Nevertheless, optimizing for efficiency is not useless and in the right place, a constant factor can make all the difference. Base64 will turn your 3GB download into a 4GB one. More importantly, I am treating this endeavor as much as an academic as a practical one, asking could we as much as do we want to. So below is the answer I came up with.

The idea is to break binary data into chunks of uniform size. I chose 4096 bytes rather arbitrarily. Allow one final chunk of variable length and encode that one in Base64. So every 4kB, there is one character (#) which means another 4k coming. There need not be any such raw chunks; they are always followed by exactly one (possibly empty) Base64 string enclosed in %. Examples:

#.....#.....%ZGFmdXFp%
#.....#.....%%
%ZGFmdXFp%

This syntax is added to JSON, along with a few other extensions.

Design goals

• Stay deterministic context-free.
• Avoid escaping or re-encoding every byte in binary blobs.
• Simple grammar.
• Self-describing structure.
• Stay reasonably human-readable and human-writable.
• Minimize attack surface for bugs.

• Plus: Allow exact representation of binary floating point numbers.
• Plus: Allow strings to use any character encoding.
• Plus: Do not use newlines as syntax, allow arbitrary values to be serialized into single lines.
• Plus: Provide for easy streaming of values.

Non-goals

• Optimal size.
• Optimal speed.

Notwithstanding the goal to support efficiency with large blobs, this format is not meant to squeeze every last bit out of everything. That conflicts with self-descriptiveness and is what Protocol Buffers are for.

Characteristics

• Proper superset of UTF-8-encoded JSON.
• Types:
  • Null
  • Boolean
  • Number
  • Byte-Array
  • String
  • List (= JSON arrays)
  • Record (= JSON objects)
• Defined in ABNF.
  • ~150 lines.
  • Transcribes trivially to a PEG.
• All syntax is ASCII.
  • No other external encodings allowed.
• Strings are tagged with their encoding.
  • No tag means UTF-8.
  • JSON-style unicode escapes \u.... supported for compatibility.
    • UTF-16 surrogate pairs recognized by grammar.
    • Parsers SHOULD properly recode these for UTF-8 strings.
• Arbitrary bytes in strings via hexadecimal escapes \x...
• Numbers are arbitrary-precision rationals.
• Hexadecimal notation for numbers supported.
  • Including hexadecimal fraction and exponent notation.
• Top-level document consists of one value of any type.
  • JSON only allows arrays and objects.
• Defined syntax for top-level value streams.
  • Values terminated by newlines.
  • Allows parser for rule stream-element to simply be called repeatedly on input stream.

Example

{ "null":         null
, "boolean":      true
, "integer":      1234
, "rational":     1234.56
, "exponent":     1234.56e2
, "hexadecimal":  0x123AB.CDxE
, "bytes":        %ZGFmdXFp%
, "string":       "Hello"
, "encoding":     "Mot\xF6rhead"_latin1
, "list":         [23,"skidoo"]
, "record":       {}
}

Show me the code!

Glad you asked! The child currently carries the rather stupid working title datalang and resides in a repository here:

darcs get http://code.khjk.org/datalang/

Included is the ABNF grammar as well as a demo parser implemented in C using hammer. Oh right, hammer. Given that this post has already turned into a novel, I am going to save that for later.

PS: If anyone thinks of a better name than datalang, your suggestion is very welcome at my easily-guessed email address.

Fingerprints are so 90s

A few years back I prepared a presentation on the so-called Socialist Millionaires' Protocol (SMP) for a university seminar. SMP is a solution to the problem of key authentication devised for OTR (Off-the-Record), the system for instant-messaging encryption.

Today I held a short version of the presentation for non-mathematicians at the CCC Hamburg. For the benefit of the Internet, the awesomely hand-made slides are in English. There is also a handy hand-out with a protocol diagram.

The written presentation for the course is completely in German and math-rich. I did try hard to make it a clear read for the so-inclined. Have fun! :)

An introduction to Bitcoin

I held a little intro talk about Bitcoin last night at a local Linux meetup kinda thing. It was a light technical description of what the system is and how it works.

Here are the slides and their LaTeX sources. That is all.

Blind signature basics

I'm starting work on my diploma thesis this month. The exact topic isn't set in stone yet, but it will be something crypto. If everything goes dreamy-awesome, I'll find something nice to write about lattice-based blind signatures or somesuch. Background:

• Blind signatures are used for e-cash. I'm fascinated with e-cash.
• Lattice-based methods are candidates for quantum-resistant systems. Appearently there's lots of current research going on.
• I've done some lattice theory at Charles University in Prague. Never thought I'd see it again, so wouldn't that be something.
• There's zero knowledge in there somewhere. Another fascination.

So, time to sum up the basics. As far as my history serves, David Chaum invented blind signatures in the 80s for electronic voting but nobody wanted to buy that, so he also invented electronic cash. Then he got really paranoid and didn't sell it either. Real quick summary. ;)

Anyway…

The principle is to mix whatever you want signed (electronic voting ballot, 100 EUR banknote) with a random blinding factor and divide that out only after Trent (your government, bank) has signed. Thus Trent cannot recognize and connect the note to you when it comes back to him later.

The classic algorithm is based on RSA and is painted up fast. Unfortunately, my awesome markup language still has no fancy math support so you have to live with ASCII art:

m = message to be signed
e = public "encryption" (i.e. verification) exponent
n = public modulus
d = secret "decryption" (i.e. signing) exponent
k = blinding factor (just a random number)

x^(de) = x^(ed) = x (mod n)         -- RSA property

Alice prepares:  mk^e               -- blinded message
Trent signs:     (mk^e)^d = m^d k
Alice unblinds:  m^d k / k = m^d    -- signed message
Bob can check:   (m^d)^e = m

One might think that signing something completely blindly might be a bad idea. After all, a bank needs to know the value of the note it is signing. To ensure any desired property of the signed document, Trent can require a cut-and-choose step. In this case Alice must give him n different but equivalent messages. He chooses one of them and asks Alice to unblind all the others. Trent signs the remaining blinded one if the others satisfy the desired property. Alice's chance to cheat of 1:n can be made unattractive by attaching a suitable penalty.